【提问】下面是一个一线教师提的问题,请你给出解释.
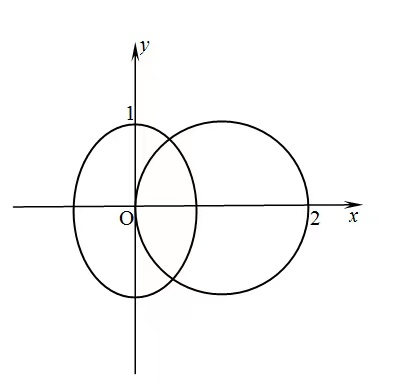
已知椭圆2x^2+y^2=1与圆C:(x-1)^2+y^2=1交于A,B两点,求A与B的横坐标.
解:设A与B的横坐标分别为x{1}, x{2},由对称性知x{1}=x{2},
由2x^2+y^2=1与(x-1)^2+y^2=1联立, ⇒(x-1)^2+1-2x^2=1,
⇒x^2+2x-1=0,
由图知x{1}=x{2},则此方程只有一根,但△>0,却有两解,为何如此?—————————————
【回复】
众所周知,我们做事都是有前提的。比如,数学里解分式方程需要验根,解函数需要考虑定义域.
同理,解方程组需要考查未知数允许值范围.所求之根不能“超标”,超了就要删除.
由椭圆方程2x^2+y^2=1知,x∈[-1/√2,1/√2],
由圆方程(x-1)^2+y^2=1知,x∈[0,2],
关于x的公共的允许值范围是x∈[0,1/√2],事实上,方程组消去y后得的方程是:
x^2+2x-1=0它有两个根:
x{1}=-1+√2∈[0,1/√2],
x{2}=-1-√2∉[0,1/√2],必须删去.
因此,关于x的方程只有一个根,也就是说,椭圆与圆的交点的横坐标只有一个,即x=√2-1.