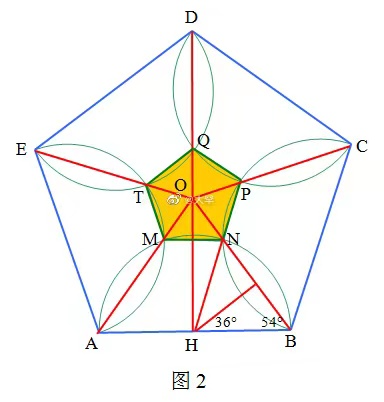
两个正五边形和五个半圆,求蓝色区域(大正五边形)与橙色区域(小正五边形)面积之比
如图1,两个正五边形和五个半圆,求蓝色区域(大正五边形)与橙色区域(小正五边形)面积之比.【大罕解答】 正五边形ABCDE、MNPQT有共同的中心O,设AB=a, 作DH⊥AB于H,由对称性可知点Q、O均在DH上,且P、N、H三点共线,PH//BC,如图2, 在△BHN中,∠BHN=72°, ∴BN=asin36°, 又OB=a/(2sin36°), ∴ON/OB=(O...
数学趣解
2022-09-29 PM
okhttpclient 报 java.io.IOException: unexpected end of stream
今天使用okhttpclient向设备上发信息,错误提示:java.io.IOException: unexpected end of stream原因是对方没有正确处理header中的Connection字段所致,经过whistle抓包后发现:Connection = keepalive,但对方没有处理这个值,默认是关闭链接,而客户端还是根据这个值去发起请求。处理办法:使用Connecti...
数学趣解
2022-09-29 PM
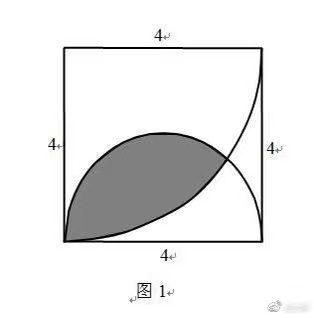
如图,边长为4的正方形,以一个顶点为圆心、4为半径作一个1/4圆的扇形,以一条边为直径作一个半圆,扇形和半圆形交错部分即阴影部分,求阴影部分的面积
有一道题:如图,边长为4的正方形,以一个顶点为圆心、4为半径作一个1/4圆的扇形,以一条边为直径作一个半圆,扇形和半圆形交错部分即阴影部分,求阴影部分的面积。有意思的是,有人断言该题无初等解法,之后果然有人给出了定积分法。实际上,本题实实在有一个初等方法,就是人们司空见惯了的割补法。具体算式是: ️ (1/2) ×2arctan2×(1/2) ×2arctan(1/2) ×16-8, ...
数学趣解
2022-09-29 PM