用的马尔可夫概率转移过程期望值求解方法 - yuange
马尔可夫过程##通用的马尔可夫概率转移过程期望值求解方法好像搞定了任意连通图的任意转移概率的马尔可夫过程的路径期望值计算,包含多结束点以及每条边带加权路径期望值计算。这电路图里面引入“升压器”的概念就行。如果每个顶点的边数bn,每条边转移概率都相同就是1/bn,那就是很简单的电路图,很好计算,其实只要每条边的两个端点的pkbn相等,这条边换成pkbn条边连接就行,或者理解化成这条边的电阻为1/(pk*bn)。少量边两端的pk*bn不相等,这条边中间引入升压器概念连接起来,其它相等的边正常按正常电阻连接,然后按电路图计算就行。复杂点的桥式电路,可以用星形和Y行的电路转换。如果不相等的太多,...
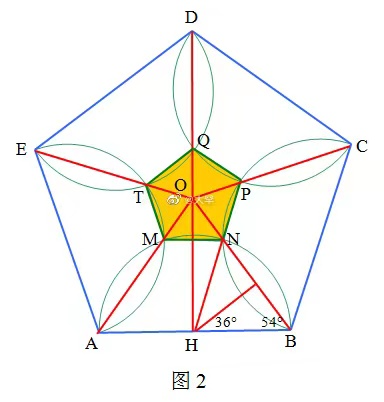
两个正五边形和五个半圆,求蓝色区域(大正五边形)与橙色区域(小正五边形)面积之比
如图1,两个正五边形和五个半圆,求蓝色区域(大正五边形)与橙色区域(小正五边形)面积之比.【大罕解答】 正五边形ABCDE、MNPQT有共同的中心O,设AB=a, 作DH⊥AB于H,由对称性可知点Q、O均在DH上,且P、N、H三点共线,PH//BC,如图2, 在△BHN中,∠BHN=72°, ∴BN=asin36°, 又OB=a/(2sin36°), ∴ON/OB=(OB-BN)/OB =1-BN/OB=1-2(sin36°)^2=cos72° =(√5-1)/4, ∴S(ABCDE)/S(MNPQT)=(OB/ON)^2 =[4/(√5-1)]^2...
okhttpclient 报 java.io.IOException: unexpected end of stream
今天使用okhttpclient向设备上发信息,错误提示:java.io.IOException: unexpected end of stream原因是对方没有正确处理header中的Connection字段所致,经过whistle抓包后发现:Connection = keepalive,但对方没有处理这个值,默认是关闭链接,而客户端还是根据这个值去发起请求。处理办法:使用Connection = close传输值。private static class NetInterceptor implements Interceptor { @Override ...
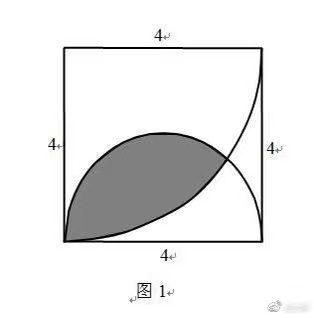
如图,边长为4的正方形,以一个顶点为圆心、4为半径作一个1/4圆的扇形,以一条边为直径作一个半圆,扇形和半圆形交错部分即阴影部分,求阴影部分的面积
有一道题:如图,边长为4的正方形,以一个顶点为圆心、4为半径作一个1/4圆的扇形,以一条边为直径作一个半圆,扇形和半圆形交错部分即阴影部分,求阴影部分的面积。有意思的是,有人断言该题无初等解法,之后果然有人给出了定积分法。实际上,本题实实在有一个初等方法,就是人们司空见惯了的割补法。具体算式是: ️ (1/2) ×2arctan2×(1/2) ×2arctan(1/2) ×16-8, ️ 2π+12arctan(1/2)-8 . 一般地,设正方形边长为2d,那么 S阴影=S1+S2-2S3, 以下分别计算S1,S2,S3,从而可得 S阴影=(1/2)(d^2)[...
GDB加载/卸载so时断下来的方法及步骤
给bluerust推销「DTrace on Windows」,他顺嘴说费了好一会儿才在gdb python里实现sxe等价功能。当时我也顺嘴问了一句,你是想sxe啥?他说原始需求是「模块一加载,在指定偏移下一个断点」。当时我想他怕是有啥高级需求要满足,才动用gdb python。单就这个需求,我一般catch commands写一段,比如catch load some commands $bpnum tb *some+off commands $bpnum silent set *(unsigned int*)($rcx+0x200)=$r...