查看指定进程的环境变量 - scz
Q:用如下命令启动Firefox后,想确认SSLKEYLOGFILE位于目标进程环境变量中SSLKEYLOGFILE=$HOME/src/sslkey.log firefoxA: scz 2022-10-25获取PIDps auwx | grep firefoxpidof firefox显示指定PID的环境变量strings /proc//environ | grep SSLKEYLOGFILExargs -0 -n 1 echo < /proc//environ | grep SSLKEYLOGFILExargs -0 -L 1 -a /proc//environ | grep ...
【题目】对正整数n,记I(n)={1,2,3,…,n},P(n)={m/√k|m∈I(n), n∈P(n)} - 大罕
本文适合于高一学生. 【题目】对正整数n,记I(n)={1,2,3,…,n},P(n)={m/√k|m∈I(n), n∈P(n)}, ⑴求集合P(7)中元素的个数; ⑵若P(n)的子集A中任意两个元素之和不是整数的平方,则称 为“稀疏集”,求n的最大值,使P(n)能分成两个不相交(即交集为空集)的稀疏集的并. 【解答】 ⑴对于集合P(7),I(7)={1,2,3,…,7}. 当k=1,2,3,5,6,7时,P(7)={m/√k|m∈I(n)}分别有7个元素,计7×6=42个; 当k=4时,P(7)={m/2|m∈I(n)}={1,2,3,1/2,3/2,5/2,...
正三角形外一点到三顶点距离为定值问题-大罕
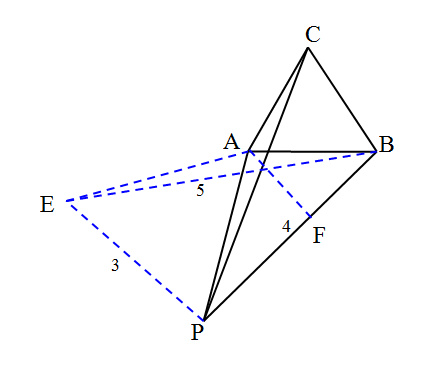
正三角形内一点到三顶点距离为定值,此题前文利用旋转已解决.自然要问:正三角形外一点到三顶点距离为定值,如何解决? 内外有别吗? 【问题】正三角形ABC外一点P,已知PA=3,PB=4,PC=5,求△ABC的面积. 【解答】将△ACP绕点A沿逆时针旋转60°得到△ABE,如图. 则BE=CP=5,由∠EAP=∠BAC=60°,且EA=PA,知△EAP为正三角形, 故EP=PA=3,又PB=4,由勾股定理逆定理知∠BPE=90°,∴∠APB=90°-60°=30°,过点A作AF⊥PB于点F,AF=(1/2)PA=3/2,PF=3√3/2, 在Rt△AFB中, AB^2=A...
求出了所有维度的半球的通解。- yuange
p(m,n)=s(m-1,n-1)/2^(n-1)=1/2^(n-1) ΣC(n-1,k) ,k从0到m-1求和。C(n,k)=n!/((n-k)!k!),组合公式,其中特别的:C(n,0)=1,k>n,C(n,k)=0。p(1,n)=1/2^(n-1)p(2,n)=(1+n-1)/2^n=n/2^(n-1)p(3,n)=(1+(n-1)+(n-1)(n-2)/2!)/2^(n-1)=(1/2(n^2-n+2))/2^(n-1)=(n^2-n+2)/2^n圆里更一般性的圆弧的通解:圆里随机n个点,都在q*2π幅度的圆弧里的概率:p(n,q)=n*q^(n-1) . 0<=q...
从内存中直接加载执行ELF - scz
参看Using eBPF to uncover in-memory loading - Pat H [2021-02-15] https://blog.tofile.dev/2021/02/15/ebpf-01.html作者给了一个完整示例,从内存中直接加载执行ELF。bluerust推荐过memfd_create,但我现在很少用C编程,未实践过。Pat H给了Python版示例,演示效果极佳。假设WEB服务在此cp /usr/bin/id . python3 -m http.server -b 192.168.65.25 8080在客户端验证WEB服务正常curl -s http://...